Resource Centers
Taguchi Experiments
Dr. Genichi Taguchi
- Dr. Taguchi built on the work of Plackett and Burman by combining statistics and engineering to achieve rapid improvements in product designs and manufacturing processes.
- His efforts led to a subset of screening experiments commonly referred to the Taguchi Techniques or the Taguchi Method®.
Major Premises of Taguchi Techniques
- Focus on the robustness of the product.
- Make the product correctly in spite of variation in materials and processes.
- Design the product to be insensitive to the common cause variation that exists in the process.
- Quantify the effects of deviation using the Quality Loss Function
- The Quality Loss Function, L(y), provides both a conceptual and a quantifiable means to demonstrate the impact of deviation from target.
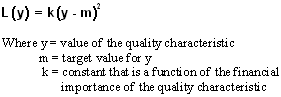
Noise Factors
- Taguchi calls common cause variation the “noise.”
- Noise factors are classified into three categories: Outer Noise, Inner Noise, and Between Product Noise.
- Taguchi’s approach is not to eliminate or ignore the noise factors; Taguchi techniques aim to reduce the effect or impact of the noise on the product quality.
Quality Loss Function
- The Loss Function can help put the cost of deviation from target into perspective.
- The loss represents a summation of rework, repair, warranty cost plus customer dissatisfaction, bad reputation, and eventual loss of market share for the manufacturer.
Signal to Noise Ratio
- Taguchi’s emphasis on minimizing deviation from target led him to develop measures of the process output that incorporate both the location of the output as well as the variation. These measures are called signal to noise ratios.
- The signal to noise ratio provides a measure of the impact of noise factors on performance. The larger the S/N, the more robust the product is against noise.
- Calculation of the S/N ratio depends on the experimental objective:
- Bigger-the-Better
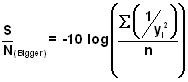
- Smaller-the-Better
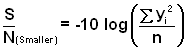
- Nominal-is-Best
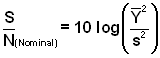
Derivation of Taguchi Matrices
- Taguchi matrices are derived from classical Full Factorial arrays.
- As with Plackett-Burman designs, Taguchi designs are based on the assumption that interactions are not likely to be significant.
- Taguchi designs have been developed to study factors at two-levels, three-levels, four-levels, and even with mixed levels.
- The levels in Taguchi matrices have historically been reported as Level 1 and Level 2 for two-level experiments.
- These levels are no different than the Low (-) Level and the High (+) Level used in Full Factorial designs and by Plackett and Burman.
- For more than two levels, experimenters typically use Level 1, Level 2, Level 3, etc. for Taguchi designs.
Types of Taguchi Designs
- A series of Taguchi designs for studying factors at two-levels are available.
- Two-level designs include the L4, L8, and L16 matrices.
- The L4 design studies up to 3 factors.
- The most popular Taguchi designs are the L8 and L16 that study up to 7 and 15 factors respectively.
- The L4, L8, and L16 designs are geometric designs based on the 22, 23, and 24 Full Factorial matrices respectively. They are based on the Full Factorials so that interactions can be studied if desired.
- Non-geometric Taguchi designs include the L12, L20, and L24 designs that can study up to 11, 19, and 23 factors respectively.
- There are other two-level Taguchi Matrices, both geometric and non-geometric, designed to study even more factors, but it is rare that larger numbers of factors can be studied in a practical, feasible, or cost-effective manner.
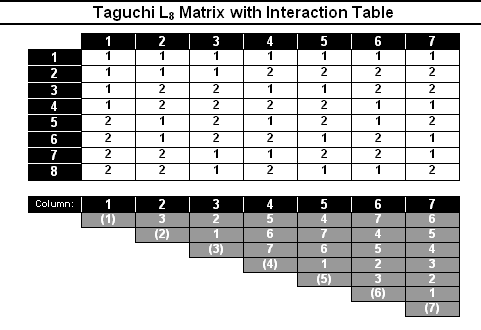
Analysis of Interactions
- While Taguchi views interactions as noise factors and most likely not significant, he does offer techniques to evaluate the impact of two-way interactions on responses.
- Taguchi provides two techniques to explore interactions in a screening experiment.
- The linear graph is a graphical tool that facilitates the assignment of factors and their interactions to the experimental matrix.
- Some experimenters find the interaction tables developed from the linear graphs to be easier to use.
Three-Level Matrices
- Taguchi screening designs for three levels exist.
- The L9 looks at 4 factors at 3 levels.
- An L27 can be used to study up to 13 factors at 3 levels and an L81 can evaluate up to 40 factors at 3 levels.
- Taguchi designs for 4 levels and 5 levels are available.
Matrices with Outer Arrays
- The use of outer arrays provides a means to separate the impact of the process or product factors from the noise factors.
- The standard matrix is used as an inner array to study the process/product factors and an outer array for evaluating one or two noise factors is added.


