R&R Analysis Using ANOVA

Analysis of Variance, or ANOVA for short, is an experimental design technique that looks at a number of variables at the same time.

• It is used to help determine which of the variables under study have a statistically significant impact on the process output.
• With measurement systems, we can explore how the test equipment and appraiser variables affect the measurement system output.

ANOVAs allow us to study four measurement system components:

• Variation between parts or samples.
• Reproducibility between operators or appraisers.
• Repeatability of the measurement equipment.
• Interaction between the samples and the appraisers.

The use of ANOVA does have some advantages over standard GR&R studies:

• ANOVAs provide information on interactions between samples and appraisers.
• With an ANOVA, we can vary the number of samples, appraisers, trials, and even the number of measurement devices to get a more accurate picture of the variation in the measurement system.
• ANOVAs allow us to get an accurate estimate of variances.
• ANOVA techniques are the preferred method for analyzing measurements for destructive testing.

Disadvantage of ANOVA:

• Calculations using ANOVA are more complex than those with other techniques. It is best to use a computer with DOE software for the calculations.

ANOVA Data Format

• A standard 2-factor ANOVA format is used for analyzing measurement systems.
• Factor A is used to designate the parts or samples. Factor B represents the appraisers.
• The number of levels for each factor is a function of the number of samples and the number of appraisers.

ANOVA Table

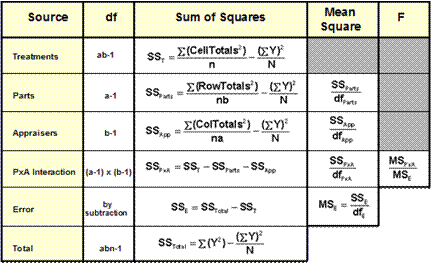
Where:

a = number of levels of a

b = number of levels of b

n = sample size per cell

N = total number of measurements made

Mean Square Values

• Mean square values are calculations of variance. The variance is the standard deviation squared.
• Mean square values are calculated for the Parts (MS_Parts), Appraisers (MS_Appraisers), the Parts x Appraisers Interaction (MS_PxA), the Error (MS_Error), and a “Pooled” term MS_Pool, if appropriate.

PxA Interaction

• We will evaluate the significance of the Parts x Appraisers Interaction using the F-test.
  • If this interaction is significant, we will need to investigate the reasons for it.

• If it is not significant, we will assume it is really part of the experimental error and pool the PxA Interaction value in with the Error Value.

Calculating Repeatability

• If the PxA Interaction is not significant, then the Repeatability statistic, s_E, is determined by pooling the MS_Error and MS_PxA.

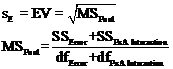
• If the interaction is significant, then the Repeatability statistic, s_E, is determined from the MS_Error

Calculating Reproducibility

• The Reproducibility, s_A, is determined by the MS_Appraisers with a correction term to account for confounding from the instrument variation.
• If the PxA Interaction is not significant:

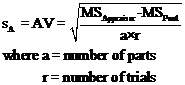
R&R Calculations

• If the PxA Interaction is not significant, the R&R is simply:

• If the PxA Interaction is statistically significant, the R&R calculation is more involved:

where:

r=number of trials

R&R as a % of the Total Tolerance (TT)

• We prefer the measurement system to take up less than 10% of the Total Tolerance. If it takes up 30% or more of the TT, the measurement system needs work.

R&R as a % of the Total Variation (TV):

• If the %GR&R is greater than 30% of the total variation, then the measurement system should be improved.
• To calculate the percentage of the total variation taken up by the measurement system, we need to know both the Part Variation (PV) and the Total Variation, TV.
• If the PxA Interaction is significant:

• If the PxA Interaction is not significant:

• With PV known, TV can be calculated:

Contribution of MSA to Total Variation:

• We can also calculate the contribution that the measurement system actually makes to the total variation. The formula for the % Contribution is: